[Stan][Python] 線形重回帰でオゾン量の予測モデルを作成する

はじめに

前回はPystanの導入として線形単回帰モデルを用いて米国女性の体重と身長の関係を説明するモデルを作成してみました。今回はオゾン量のサンプル・データを題材にしてそれを説明する線形重回帰モデルを作成してみます。また、線形重回帰モデルを作成するにあたってのデータの検討方法も紹介します。Pystan、Stan等については前回記事を参照してみてください。

線形重回帰モデル

線形重回帰モデルは目的変数と複数の説明変数に相関が認められる場合のモデリング手法です。以下の様な複数の説明変数 \( X_1, \dots, X_n \) に傾き \( \beta_1, \dots, \beta_n \) をそれぞれつけ、それに切片 \( \beta_0 \) をあわせたものが目的変数 \( Y \) を記述するモデルです。

[latex] Y = \beta_0 + \sum^n_{i=1} \beta_i X_i + \epsilon [/latex]

前回と同様、ここでの \( \epsilon \) は平均0, 分散 \( \sigma \) のガウス分布 \( N \) に従います

[latex] \epsilon \sim N(0, \sigma) [/latex]

これらの関係を一つにまとめると

[latex] Y \sim N(\beta_0 + \sum^n_{i=1} \beta_i X_i, \sigma) [/latex]

のようになります。

データセット

今回もR向けに提供されているデータ・セットの中から、1973年におけるニューヨークの大気状態観測値のデータ・セットを用います。

このデータ・セットを用いてモデリングをしていきますが、まずこのデータ・セットの特徴を見て、そこから重回帰を行うための説明変数のフィルタリングを実施します。

重回帰モデリングの下準備

重回帰モデリングを行うにあたって、対象となるデータについて、変数すべての間に相関があるようなものであればいいのですが、現実的にはそのようなデータばかりではないです。このため、重回帰を行う前に与えられたデータ・セットについての相関を変数の対毎に把握する必要があります。

そのために相関行列・対散布図等を計算、図示することで与えられた変数同士の相関関係を確認できます。

• 相関行列 : 与えられた変数同士の相関係数を成分とする行列です。例えば変数 \( x, y, z \) のデータについては以下の様な相関行列が定義されます。

[latex] R = \left( \begin{array}{ccc} 1 & r_{xy} & r_{xz} \\ r_{yx} & 1 & r_{yz} \\ r_{zx} & r_{zy} & 1 \end{array} \right)\\ [/latex]

ここで、 \( r_{xy} ( = r_{yx}), r_{xz} ( = r_{zx}), r_{yz} ( = r_{zy}) \) は下記のように標本データから算出される相関係数です。

[latex] r_{xy} = \frac{\sum^n_{i=1}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{(\sum^n_{i=1}(x_i - \bar{x})^2)(\sum^n_{i=1}(y_i - \bar{y})^2)}} [/latex]

• 対散布図 : 与えられた変数同士の相関をひと目で把握するために、標本データの２つの変数の関連を片方の変数を縦軸、もう片方の変数を横軸としてグラフにプロットしたものです。例えばデータ分析のサンプルとしてよく用いられるiris(アヤメ）データ・セットで作成された対散布図は以下のようになります。

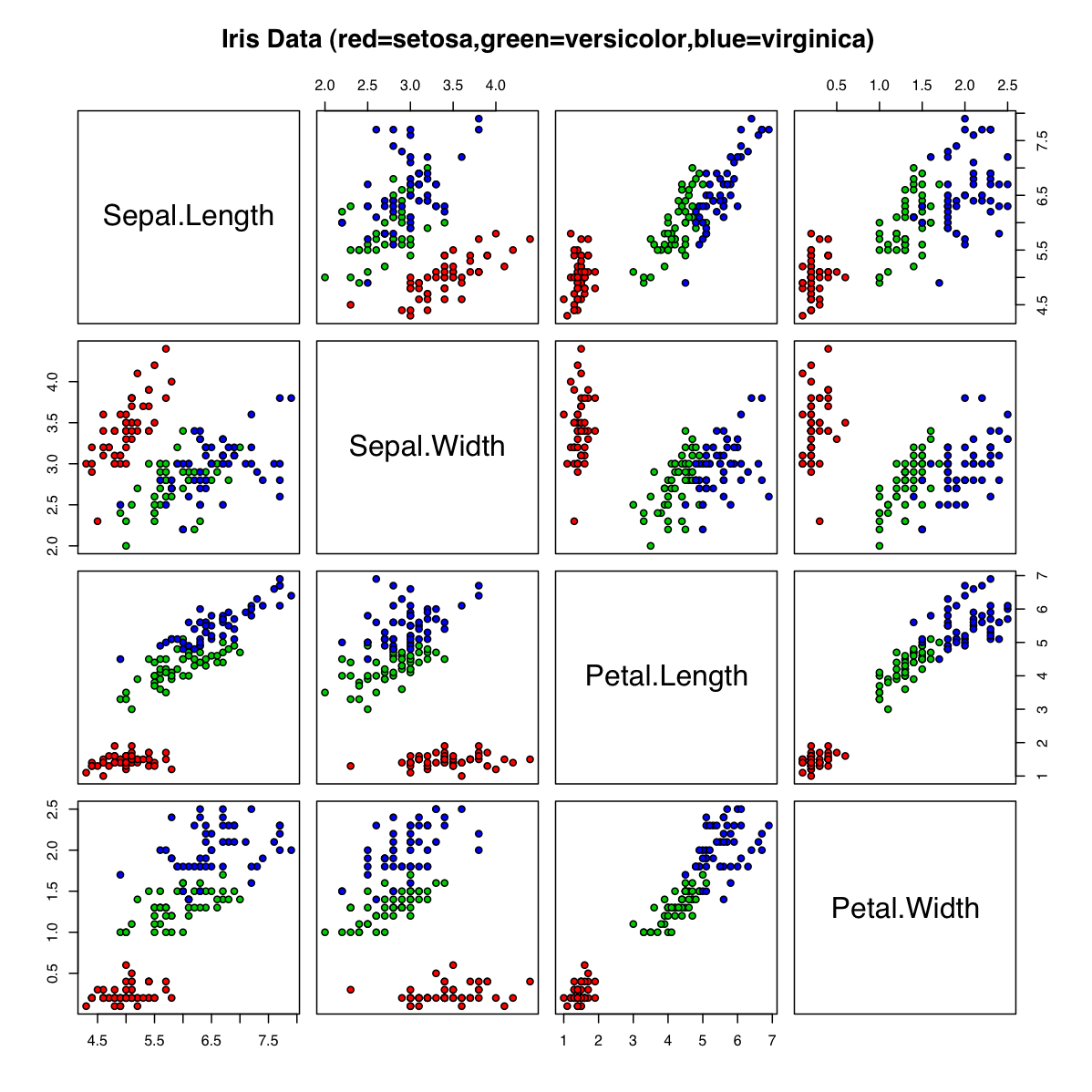
この図からはPetal.Length変数とPetal.Width変数に明確な相関があることが見て取れます。

今回はデータ分析周りのツールキットライブラリであるpandasを用いて対散布図を図示してみます。

対散布図の図示

今回のサンプルコードはこちらに上がっています。

前回と同様にjupyter notebook上でデータ・セットのインポートから計算までを行います。

$ jupyter notebook

jupyter notebook実行環境と同一のディレクトリにデータ・セットのテキストファイルを置きます

airquality.tsv

    Ozone   Solar.R Wind    Temp    Month   Day
1   41  190 7.4 67  5   1
2   36  118 8   72  5   2
3   12  149 12.6    74  5   3
4   18  313 11.5    62  5   4
...

ここでnotebook上で下記のサンプルを動作させてみてください

In [1] :

import pystan
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
from pandas.tools.plotting import scatter_matrix

ozone = pd.read_csv("airquality.tsv", sep="\t", index_col=0, usecols=[0, 1, 2, 3, 4])

scatter_matrix(ozone, figsize=(10, 10))

• l8 : tsvファイルからオゾンサンプル・データを変数に展開しています。read_csv 関数はpandas内で用いられるDataFrameという二次元のラベル付されたDBのテーブルのようなデータ形式に入力したファイルの中身を展開します。

• l10 : scatter_matrix 関数はDataFrameの中身を対散布図として表示してくれます。figsizeで図のサイズも指定できます。

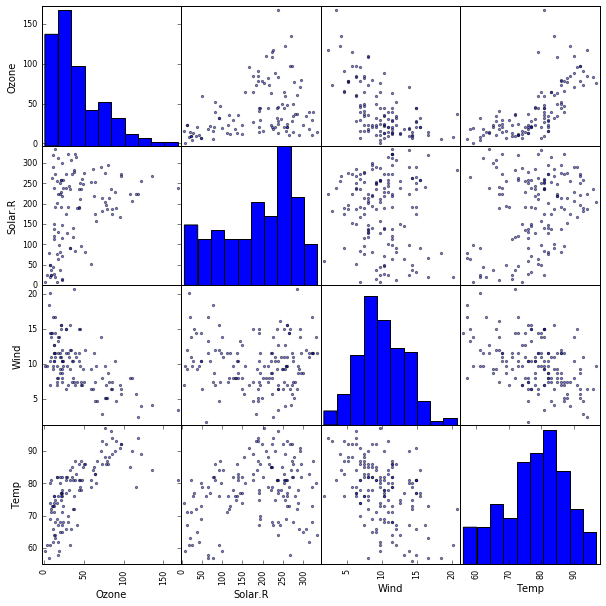
出力として下記のような図が表示されます。

Out [1] :

重回帰モデルの構築

先のアヤメデータほど明瞭ではないですが、相対的なデータの散らばり具合からすると、先ほどの図からはOzone変数とWind変数の間、Ozone変数とTemp変数の間に相関がありそうだということが読み取れ、下記のような重回帰モデルが想定されます。

[latex] Y_{\text{ozone}} \sim N(\beta_0 + \beta_{\text{wind}} X_{\text{wind}} + \beta_{\text{temp}} X_{\text{temp}}, \sigma) [/latex]

この仮定のもと、実際にStanでモデルを組み、前回と同様にjupyter notebook上でpystanからモデルのパラメータを予測し、実際のデータとの突き合わせを行ってみます。

In [2] :

model = """
data {
  int<lower=0> N;
  vector[N] temp;
  vector[N] wind;
  vector[N] ozone;
}
parameters { 
  real beta_0;
  real beta_wind;
  real beta_temp;
  real<lower=0> sigma;
}
model { 
  ozone ~ normal(beta_0 + beta_wind * wind + beta_temp * temp, sigma);
}
"""

Stanのモデルコードをmodel変数に代入しています。

In [3] :

filtered_datum = datum.dropna()
datum_array = np.transpose(filtered_datum.reset_index().values)
ozones = datum_array[1]
winds = datum_array[3]
temps = datum_array[4]

• l1 : datum.dropna() ではDataFrameのなかでレコードにNaNが含まれるものを取り除いています。
• l2 : datum_arrayにはNaNが取り除かれたDataFrameからnumpyのarrayを構成しています。filtered_datum.reset_index().valuesでDataFrameからレコード毎に各カラムの値が配列として格納され、さらにそのレコードを表す配列を集めた配列として格納されますが、これの転置をとるためにnp.transposeし、後にインデックスでのアクセスでカラム毎の値の配列を取得できるようにしてあります。

• l3-5 : オゾン量、風量、温度の観測結果をそれぞれ配列として変数に展開しています。

In [4] :

fit = pystan.stan(model_code=model, data=dict(temp=temps, wind=winds, ozone=ozones, N=len(temps)))

stanのコードから重回帰モデルを作成し、実際のデータからパラメータをベイズ推定しています。結果はfit変数に展開されます。

In [5] :

fit

fit変数に格納された結果を見てみます。

Out [5] :

Inference for Stan model: anon_model_9046ea6597d9f0d22691262a7389930b.
4 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=4000.

            mean se_mean     sd   2.5%    25%    50%    75%  97.5%  n_eff   Rhat
beta_0    -67.24    0.93  23.19 -111.7 -82.74 -67.35 -51.77 -21.25  618.0    1.0
beta_wind  -3.29    0.02   0.66  -4.59  -3.74   -3.3  -2.86  -1.96  768.0    1.0
beta_temp   1.83  9.9e-3   0.25   1.32   1.66   1.83    2.0   2.31  634.0   1.01
sigma      22.02    0.05   1.55  19.28  20.93  21.94  22.98  25.32  840.0    1.0
lp__      -394.6    0.05   1.44 -398.4 -395.3 -394.3 -393.6 -392.9  750.0    1.0

Samples were drawn using NUTS(diag_e) at Tue Jul  5 12:53:11 2016.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

ベイズ推定で予測されたパラメータとしては下記のようにその平均値を解釈できることがわかりました。

[latex] \bar{\beta_0} = -67.24, \ \bar{\beta}_{\text{wind}} = -3.29, \ \bar{\beta}_{\text{temp}} = 1.83 [/latex]

ベイズ推定によるパラメータの分布も見てみます。

In [6]:

fit.plot()

Out [6]:

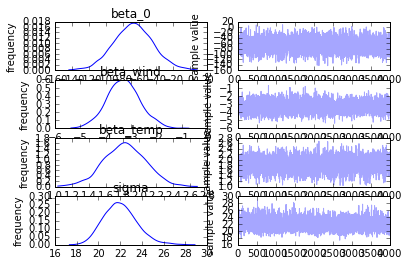
図が潰れて少々読み取りづらいですが、おおかた先ほど式で示されたパラメータ平均値の周りに分布していることがわかります。

次に実際のデータとの突き合わせを行っていきます。

In [7]:

samples = fit.extract(permuted=True)
beta_0 = np.mean(samples["beta_0"])
beta_wind = np.mean(samples["beta_wind"])
beta_temp = np.mean(samples["beta_temp"])

前回と同様にサンプリングされたパラメータの平均値をとることで予測重回帰モデルの各パラメータとします。

In [8]:

from mpl_toolkits.mplot3d import Axes3D

def show_with_angle(angle):
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    ax.view_init(elev = 10., azim = angle)
    x = np.arange(0, 20, 0.5)
    y = np.arange(60, 100, 1.0)
    X, Y = np.meshgrid(x, y)
    Z = beta_0 + beta_wind * X + beta_temp * Y
    surf = ax.plot_surface(X, Y, Z, rstride = 5, cstride = 5, alpha = 0.4)
    ax.set_zlim(0, 150)
    ax.scatter(winds, temps, ozones, c='green', marker='o', alpha=1)
    ax.set_xlabel('Wind')
    ax.set_ylabel('Temp')
    ax.set_zlabel('Ozone')
    plt.show()

show_with_angle(0)
show_with_angle(30)
show_with_angle(50)
show_with_angle(70)
show_with_angle(90)
show_with_angle(110)

ここでは三次元上に先ほど算出したパラメータを元に構成された重回帰モデルを平面として表示（z方向をozoneとして）、さらに実際のデータがどの位置にあるかをプロットしてみて、カメラの向きを変えながらどの程度実際のデータを重回帰モデルがよく記述しているか見ています。各行での処理の説明を記します。

• l1: matplotlibで3d空間上に描画するためのコンポーネントをインポートします。
• l3: 3d空間上でカメラの角度を指定して各種データを描画するための関数です。
• l4: plt.figure()でなにも描画されていない新しいウィンドウを作成します。
• l5: 3次元空間上でのサブプロットをウィンドウに作成します。
• l6: カメラの位置を指定します。elevはz軸から見た仰角、azimはxy平面上での方位角を示します。azimに関数のangle引数を代入することでさまざまな方位角からプロット結果を見れるようになっています。
• l7-9: x, y軸上での座標位置をndarrayとして展開し、xy平面上に等間隔に並べられたメッシュ点として網羅されるよう行列の変数X, Yに値が展開されます。（参考：【Python】ふたつの配列からすべての組み合わせを評価 - keisukeのブログ）
• l10: xy平面上の各メッシュ点における重回帰モデルの予測値を変数Zに行列として展開します。
• l11: 重回帰モデルの予測値を平面としてプロットします。平面としてプロットする際の線間隔を rstride, cstrideで定義できます。
• l12: z軸で表示する範囲を定めます。
• l13: 実際のデータを緑色でプロットします。
• l14-16: 各軸のラベルの名前をつけています。
• l17: プロットを表示します。
• l19-24: 方位角を変えてあらゆる角度から見た3D図を表示します。

Out [8]:

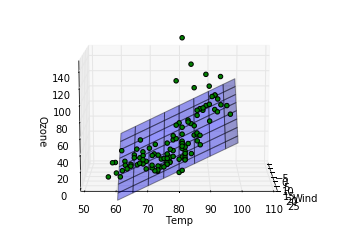
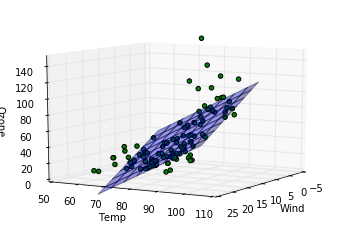
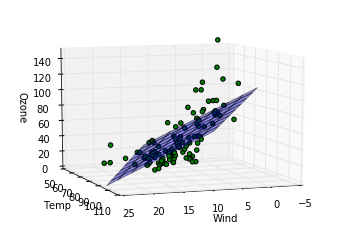
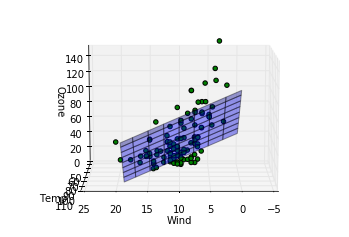
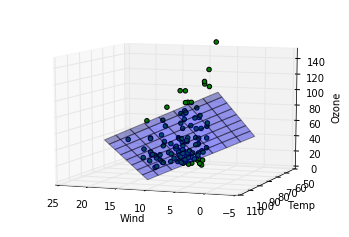
完全にとまではいかないまでもおおかたのデータについてはわりと重回帰モデルを表した平面の周りにあることが見て取れます。

重回帰モデルまわりの概念

多重共線性

重回帰モデルによるモデリングを行う際に対象にしようとしている説明変数同士に相関がある場合があります。重回帰モデルでの仮定として、変数同士が互いに独立という前提条件があり、そうでない場合は係数のパラメータに対して予測が難しくなります。数学的な話でいうと、説明変数 \( X_1, \dots, X_n \) 同士のどれか一組が独立でない（線形な関係がある）場合、モデルの前提となる

[latex] Y = \beta_0 + \sum^n_{i=1} \beta_i X_i [/latex]

式のパラメータ\( \beta_0, \dots, \beta_n \)を求める際に実際のデータで作成される行列の逆行列が存在しない可能性が存在してしまうため、予測でもパラメータが発散するケースが起こりうるためです。

このため、説明変数同士にたいしても相関がないことを予め対散布図等で確認することが重要です。

交互作用

一つの説明変数による効果（いままでの例でいうと説明変数 \( X_i \) に依存して \( Y \) が変化する部分) が他の説明変数に応じて変化することを交互作用と呼び、重回帰モデルではこの効果も含むことができます。たとえば、先ほどのオゾンの予測モデルを例とすると、Wind値とTemp値の交互作用をモデルに含めるとすれば、以下の様なモデルの記述を仮定することになります。

[latex] Y_{\text{ozone}} \sim N(\beta_0 + \beta_{\text{wind}} X_{\text{wind}} + \beta_{\text{temp}} X_{\text{temp}} + \beta_{\text{mixed}} X_{\text{wind}} X_{\text{temp}}, \sigma) [/latex]

まとめ

今回は重回帰モデルを用いてオゾン量のサンプル・データをもとにどのカラムを説明変数として採用すべきかの判断基準を紹介し、実際にモデルを作成し、データと付きあわせて確認してみました。前回と合わせてデータ・セットの特定のカラムを説明変数として目的変数を説明する一般線形モデルのうち、単回帰と重回帰の２つを紹介しました。

重回帰の多重共線性まわりを調査していた段階での気になるテーマとして、複数のカラムのデータをもとにそれらを構成する共通の成分を探り、次数を下げる主成分分析や因子分析の手法にも興味が出てきたので次回以降それらも扱う予定です。

参考

• pandas : Python Data Analysis Library
• 金明哲 Rによるデータサイエンス - 森北出版 2007
• 【Python】ふたつの配列からすべての組み合わせを評価 - keisukeのブログ